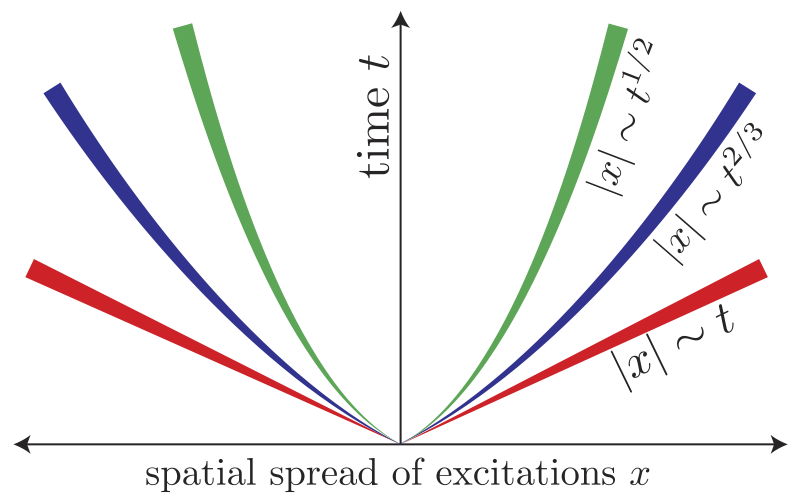
Some quantum many-body systems display emergent coarse-grained hydrodynamic behavior. Depending on the intrinsic quantum conservation laws of the system, one expects different kinds of fluid-like behaviors. Remarkably, a class of 1D quantum systems, known as integrable, possesses an infinite number of nontrivial conserved quantities which can endow them with peculiar transport properties, especially at high temperatures.

We classified the different hydrodynamic regimes for 1D quantum magnets. They are characterized by the dynamical exponent $z$, governing the length-time scaling: $z=2$ corresponds to diffusion, $z=1$ to ballistic, and $z=3/2$ to superdiffusive dynamics. The last scenario is the most puzzling. It was numerically conjectured to belong to the Kardar-Parisi-Zhang universality class in 1+1 dimensions. It is well-known in the statistical physics community to describe a wide range of phenomena like interface growth, quantum circuits, and even traffic flow. With experimentalists, we worked on observing this hydrodynamical regime with neutron scattering in a 1D spin-1/2 Heisenberg compound. We found that the spin dynamics are well described by the dynamical exponent $z=3/2$ confirming the theoretical conjecture.

In a later work, we reconciled the established low-temperature physics of the $S=1/2$ Heisenberg chain described by the Tomonaga-Luttinger liquid framework, with the recently found infinite-temperature Kardar-Parisi-Zhang superdiffusive hydrodynamics. Building on large-scale microscopic simulations, we found that they are connected by a temperature-dependent spatiotemporal crossover. As the temperature $T$ is reduced, we showed that the onset of superdiffusion takes place at longer length and time scales $\propto 1/T$.

• Collaborators: Garrett E. Granroth, Joel E. Moore, Stephen E. Nagler, Allen Scheie, Nicholas E. Sherman, Matthew B. Stone, and David A. Tennant
• Publications: Phys. Rev. B 101, 121106(R) (2020), Nat. Phys. 17, 726-730 (2021), and Phys. Rev. Lett. 127, 107201 (2021)
• Outreach: Quantum material's subtle spin behavior proves theoretical predictions and A new perspective on hydrodynamics in quantum spin chains

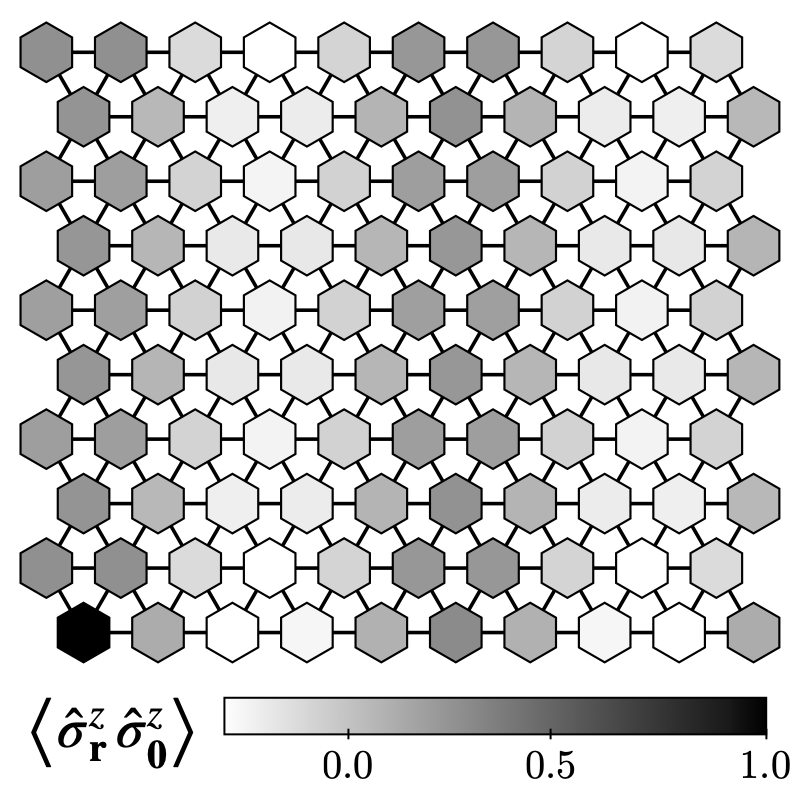
We studied what happens when one drives a paramagnetic system from a topological state to a trivial state. The only option to connect these two distinct states is via a quantum phase transition. Surprisingly, the transition never occurs as a single point when interpolating from one phase to the other. Instead, a whole new phase emerges where magnetic order settles in, sandwiched between the topological and trivial paramagnetic ones.

The most remarkable case is when the magnetic order takes the form of a stripe pattern that is incommensurate with the two-dimensional lattice. Moving to a coarse-grained picture, the interfaces between these stripes behave analogously to electric fields. They are subject to the laws of electrodynamics in the form of a deconfined $U(1)$ gauge theory.

• Collaborators: Snir Gazit and Thomas Scaffidi
• Publications: Phys. Rev. B 103, 144437 (2021) and Phys. Rev. B 103, L140412 (2021)

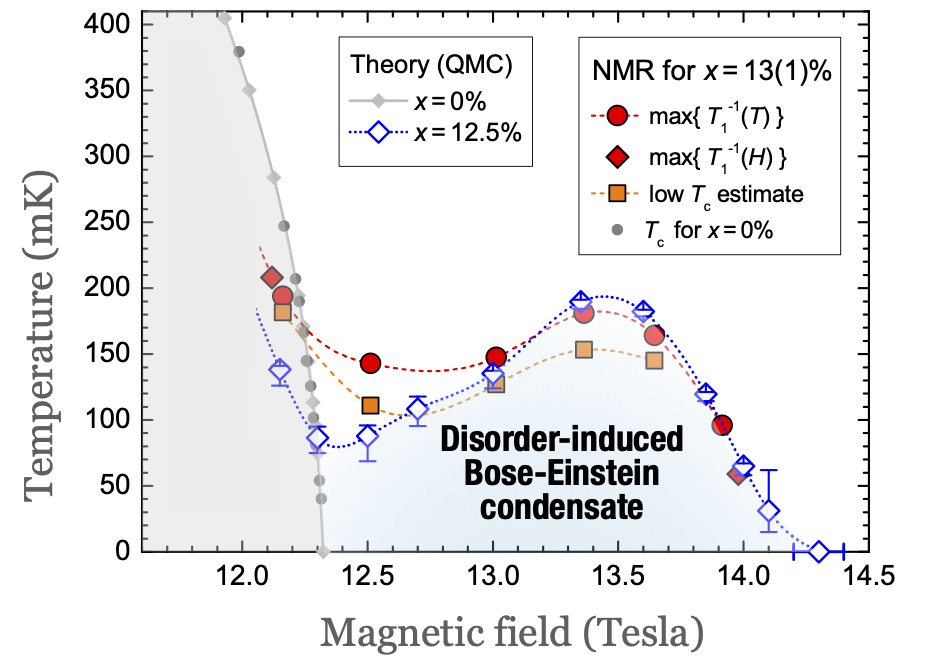
Quantum magnets can realize emergent bosonic phases of matter. Upon applying a strong magnetic field, the spin-1 compound $\mathrm{NiCl}_2-4\mathrm{SC}(\mathrm{NH}_2)_2$ realizes a Bose-Einstein condensate. Doped with $\mathrm{Br}$, randomly substituting $\mathrm{Cl}$ atoms, disorder is introduced in the form of modified exchange couplings between the spins. Randomness often diminishes the quantum coherence and can destroy it entirely if it is strong enough. Here, the disorder was believed to induce the so-called Bose glass phase: a compressible, gapless, and incoherent bosonic quantum fluid.

In collaboration with experimentalists, we investigated the interplay between disorder and interactions in this compound. Based on NMR measurements, we first built a lattice spin model for this material. Then, we addressed the stability of the Bose glass phase and found that instead of destroying the quantum coherence, the disorder induces a revival of coherence at high magnetic fields. We predicted a new, counterintuitive phase of matter: a disorder-induced Bose-Einstein condensation, and we pinned down its microscopic mechanism. It was later experimentally observed, in agreement with the theoretical model.

• Collaborators: Claude Berthier, Rémi Blinder, Sylvain Capponi, Mladen Horvatić, Edwin Kermarrec, Steffen Krämer, Nicolas Laflorencie, Hadrien Mayaffre, Anna Orlova, and Armando Paduan-Filho
• Publications: Phys. Rev. Lett. 118, 067204 (2017), Phys. Rev. Lett. 118, 067203 (2017), Phys. Rev. B 96, 024442 (2017), and Phys. Rev. Lett. 121, 177202 (2018)
• Outreach: (In French) Comment le désordre autour d’impuretés peut devenir ordre à grande échelle sous champs magnétiques intenses

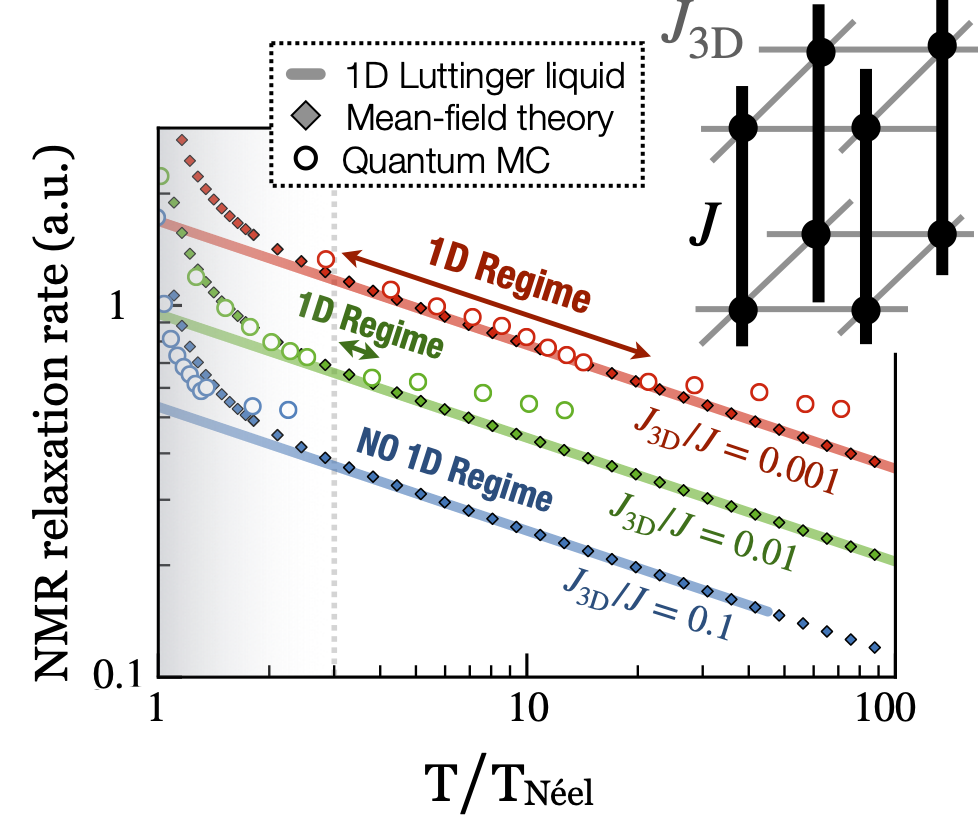
Many condensed matter probes are frequency-resolved and thus related to time-dependent quantities, e.g., neutron scattering, optical conductivity, NMR relaxation rate. It is paramount to theoretically access them and understand how they behave in different phases of matter.

We addressed this question for quantum magnets, from purely 1D systems to realistic 3D ones, by gradually increasing the strength of the coupling between spin chains. A perfect chain described by the Tomonaga-Luttinger liquid quantum field theory will result in the NMR relaxation rate diverging as a power-law with the temperature $T$ at low temperature, $\propto T^{-\alpha}$. The exponent $\alpha$ is related to a field theory parameter, which is made experimentally accessible. Because residual 3D couplings are intrinsic to materials, we studied how they affect the genuine 1D behavior, making experimental estimations of the field theory parameter more precise. A finite 3D coupling also introduces a finite-temperature phase transition in the system. We determined the behavior of the NMR relaxation around it, down to the ordered phase.

• Collaborators: Sylvain Capponi, Nicolas Laflorencie, and Edmond Orignac
• Publications: Phys. Rev. B 94, 144409 (2016) and Phys. Rev. B 98, 094403 (2018)